Long-term prediction of chaotic systems
A new deep recurrent architecture capable of learning the state evolution of various chaotic dynamical systems, substantially extending the prediction horizon.
The work on this project has published in ICDM 2022. Take a look at âWidening the Time Horizon: Predicting the Long-Term Behavior of Chaotic Systemsâ for more details.
Objective
The study of chaotic systems poses a significant challenge not only for theoretical research, but also for many practical applications. Chaotic behavior is prevalent in various nonlinear dynamical systems, including but not limited to climate dynamics, weather prediction, and the spatiotemporal dynamics of virus spread. Due to the intricate and unpredictable nature of chaotic systems, it is imperative to have a reliable solution that can handle their complex spatiotemporal dynamics and their high sensitivity to initial and boundary conditions. Achieving a high level of accuracy is crucial for numerous applications since even slight errors in the early steps of chaotic system predictions can lead to significant errors in future steps.
Proposed Model
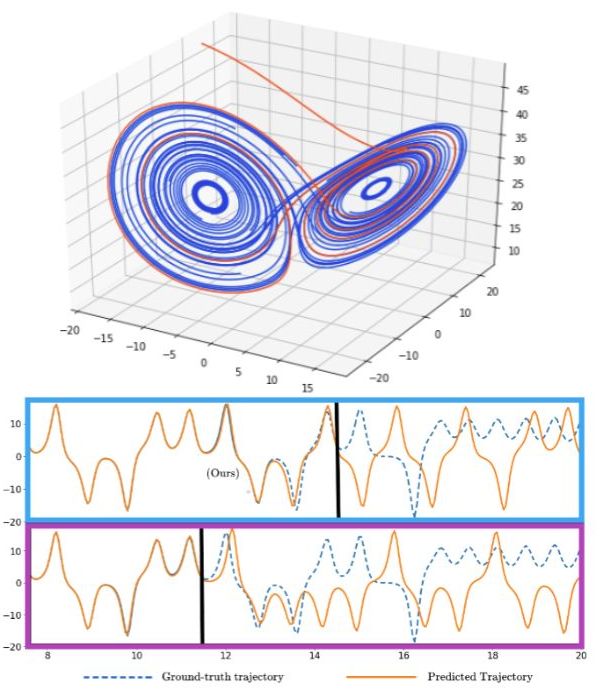
To extend the time horizon for making reliable predictions in chaotic systems, we proposed the notion of the Lyapunov Horizon Loss. This loss measures how the error divergence of a forecasting sequence evolves in a chaotic system. We developed a deep learning framework that observes the future trajectories of initial errors at a given time horizon to model the evolution of the loss up to that point. The framework has two major components:
- Error Trajectory Tracing: It utilizes a recurrent âtowerâ architecture to track the evolution of small errors in the initial conditions through phase space. This allows us to better understand the behavior of the system and make more accurate predictions about its future evolution.
- Horizon Forcing: is a training regime that optimizes the Lyapunov Horizon Loss based on short-term predictions first, and then shifts the focus to the long term as training progresses. By doing so, we can ensure that our model is capable of making reliable predictions over a longer time horizon than previous methods.
Experiments
Through the combination of these two components, our proposed model achieves a significant improvement in the accuracy of predictions for nonlinear systems. We validated our approach on three classic chaotic systems and four real-world time series prediction tasks with chaotic characteristics. Our model demonstrates superior performance compared to state-of-the-art methods.